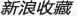①《骑士》（Horseman,1946） ②《莫比乌斯II》（Mobius II, 1963） ③《缠着魔带的立方体》（Cube with Magic Ribbons，1957）

　　梁进

　　莫比乌斯带是数学中拓扑学上的一朵“奇葩”。1858年，德国数学家莫比乌斯(Mobius，1790～1868)发现：把一根纸条的一段扭转180°后，再与另一段粘上，形成的纸带圈具有魔术般的性质。这样的纸带只有一个面，一条边，一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带就被称为“莫比乌斯带”。这个带子的奇特之处在于它本身是个二维面却只能在三维空间里展示自己的特性，如果硬要把它按在二维空间里，它只能自己穿越自己了。所以有人称它完美地展现一个“二维空间中一维可无限扩展之空间模型”。

　　埃舍尔并不是一开始就想到莫比乌斯带(Mobius Strips)的。他说：“1960年，一位英国数学家(我已经记不起他的名字了)劝我作一幅莫比乌斯带的版画。而那时我对这个东西还几乎一无所知。”然而莫比乌斯带好像就是埃舍尔带，专门为埃舍尔所生，专等埃舍尔赏识，一旦埃舍尔发现了它，它立即就成了埃舍尔的主题。埃舍尔虽然画出各种莫比乌斯带，却并不拘泥于典型的莫比乌斯带。他将其与自己擅长的镶嵌画融合，探索各种可能，达到了形形色色的奇妙效果。

　　埃舍尔的木刻画作《骑士》(Horseman)，是他在1946年完成的。在这幅画中，埃舍尔试图在二维空间里表现莫比乌斯带，但他巧妙地避开了穿越，而是用两个半周的莫比乌斯带通过一个平面连起来。带子上正反两面行走着同向却反色的骑士。本来在莫比乌斯带走的骑士走遍带子的两面都不可能改变颜色，但通过这个连接的平面，互为反色的骑士却通过埃舍尔最拿手的镶嵌而易位了！

　　再拿埃舍尔的《莫比乌斯II》(Mobius II, 1963)和《缠着魔带的立方体》(Cube with Magic Ribbons，1957)来说，前一幅画的是典型的镂空的莫比乌斯带。通过绘画技巧，在二维画布上营造一个三维空间，并在三维空间上通过一对红蚁展示莫比乌斯带的奇妙特性。这队红蚁有9只，队伍无首无尾，却一个连着一个，沿一个方向行进，布满了带子的两面，尤其诡异的是，红蚁和它的有序的队友可以肚皮贴着肚皮，相向而行。后一幅画埃舍尔利用二维对三维的视力错觉让那个缠在三维立方支架上的带子看起来好像是两个相套又分离的莫比乌斯带，又好像这两个带子是粘在一起的。带子上面连续嵌着的个个圆台好像是凸的又好像是凹的，让人玩味不已。

    来源：《中国科学报》 (2014-07-25 第20版 雅趣)