来源:联拍在线
原标题:看看他们,谁说艺术家都是数理化学渣?!
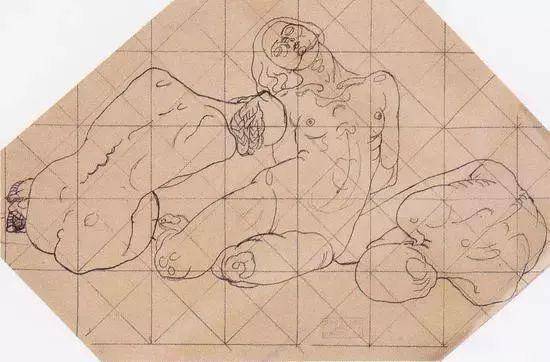 科罗曼·莫塞尔 Koloman Moser - Three Crouching Women
科罗曼·莫塞尔 Koloman Moser - Three Crouching Women学数学的人进银行,学画画的人成艺术家。生活中常有的刻板印象似乎从我们上学的时代便已开始。而实际上,不同学科之间的边界在今天已经越来越模糊。更不要提艺术和数学,因为这看似两个相聚很远的学科,其实从来就没分开过。
艺术与数学的情缘早在15世纪就已经展开。文艺复兴时期的天才达·芬奇(1452-1519)就是最鲜明的例子,这位伟大的艺术家、科学家、数学家曾经这样说,“不理解数学的人将迷失在混乱之中,不懂数学的人也读不懂我的书。”

达·芬奇的手稿中充满了各种数学公式和几何图形。
在达·芬奇众多的艺术作品中,我们都可以见到数学的应用。其中最著名的要数有着黄金分割面容的蒙娜丽莎。
 达·芬奇 Da Vinci - Mona Lisa 蒙娜丽莎
达·芬奇 Da Vinci - Mona Lisa 蒙娜丽莎《维特鲁威人》中反复出现的数字67:素描圆周长67 厘米、素描人物头手夹角67 度,素描人物耻骨横线与左右腿开退之间的夹角67 度。
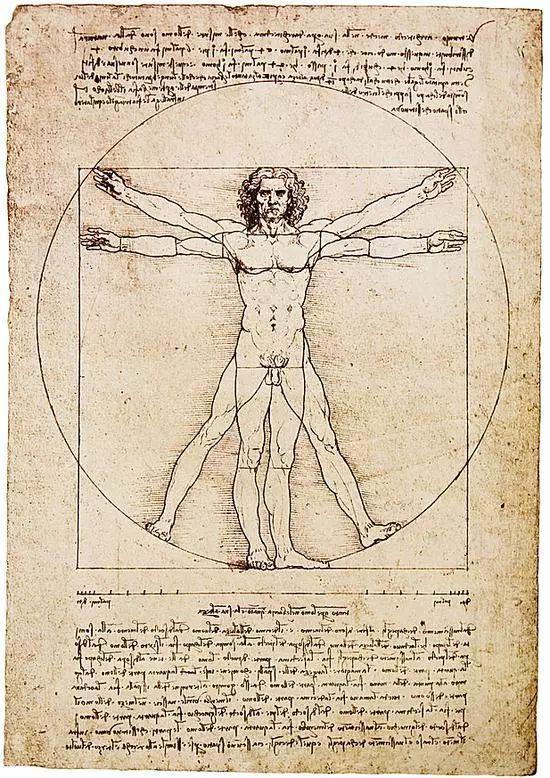 达·芬奇 Da Vinci - The Vitruvian Man 维特鲁威人
达·芬奇 Da Vinci - The Vitruvian Man 维特鲁威人他甚至还和会计学鼻祖、意大利数学家卢卡·帕乔利共同完成了《算术集成》,用手绘的插图形象直观地图解了帕乔利的数学法则。
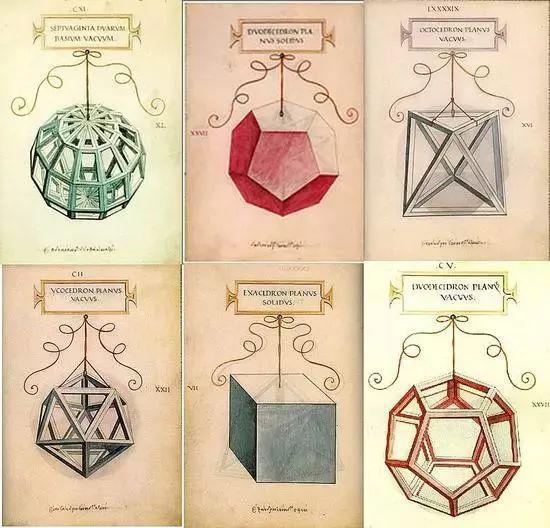
达·芬奇 Da Vinci - 《算术集成》插图
除了达·芬奇,将科学与艺术结合的还有德国人开普勒(Johannes Kepler,1571—1630)。
 YTI - 开普勒
YTI - 开普勒提起开普勒,大多数人首先都会想到他在天文学上的贡献,而同时具有数学家身份的他对“多面体”这一概念也具有极大的热情。在《Harmonices Mundi》这部书中,开普勒手绘的多面体插图极具艺术美感。
 这些精致细密的插图总让人有一种想要去填色的冲动。。。
这些精致细密的插图总让人有一种想要去填色的冲动。。。
荷兰艺术家埃舍尔(M。 C。 Escher,1898-1972)是数学艺术发展历程中相当重要的一位。他的作品多以平面镶嵌、不可能的空间、悖论、循环等作为主题,在其中可以看到对 分形、对称、双曲几何、多面体、拓扑学等数学概念的形象表达。直至今日,不仅有很多艺术爱好者,很多数学爱好者也对这位科学思维大师的作品称赞有加。
 埃舍尔 Escher - Lizard
埃舍尔 Escher - Lizard在奥地利艺术家莫塞尔(Koloman Moser,1868 - 1918)的作品中,我们可以看到相似的应用。尽管莫塞尔的作品洋溢着新艺术主义运动的色彩,但它们与几何数学的联系清晰可见。
 科罗曼·莫塞尔 Koloman Moser - by Koloman Moser
科罗曼·莫塞尔 Koloman Moser - by Koloman Moser
科罗曼·莫塞尔 Koloman Moser - by Koloman Moser
甚至连他设计的珠宝都有着浓浓的几何数学味道。
 科罗曼·莫塞尔 Koloman Moser - by Koloman Moser
科罗曼·莫塞尔 Koloman Moser - by Koloman Moser随着20世纪的展开,似乎越来越多的人开始着迷于艺术与数学的关系。曾是包豪斯高材生的马克思·比尔(Max Bill,1908-1994)相信,“数学规律是艺术的一种必须援助,只有通过数学规律,艺术家纯粹的心理世界才能最终获得恰当的形式外衣。”所以对于 数学的偏爱就十分清晰的出现在了他的创作中——不论是大量应用几何元素的平面设计;还是从莫比乌斯环得到灵感而创作的雕塑。
 By Max Bill
By Max Bill
By Max Bill
在匈牙利出生的艺术家维克托·瓦萨雷里(Victor Wasarely, 1908 - 1997)将对几何的应用拓展到了视觉错觉的范围。作为欧普艺术的奠基人,他所创造出的空间,具有闪烁和流动的效果。
 by Victor Wasarely
by Victor Wasarely
by Victor Wasarely

by Victor Wasarely
而到今天,已经没有什么能够阻挡同时热爱艺术和数学的人了。委内瑞拉艺术家Rafael Araujo将数学计算融于自己的绘画创作之中,解释自然、数学与艺术之间的关系。
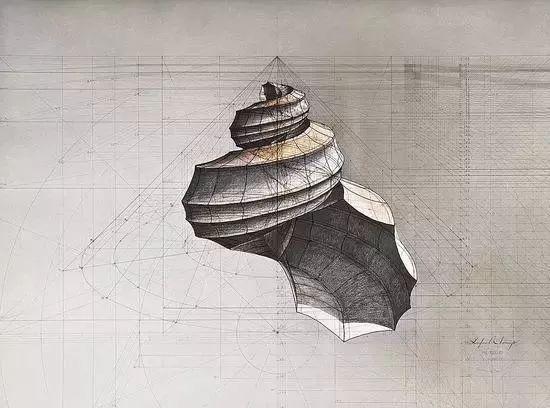
by Rafael Araujo
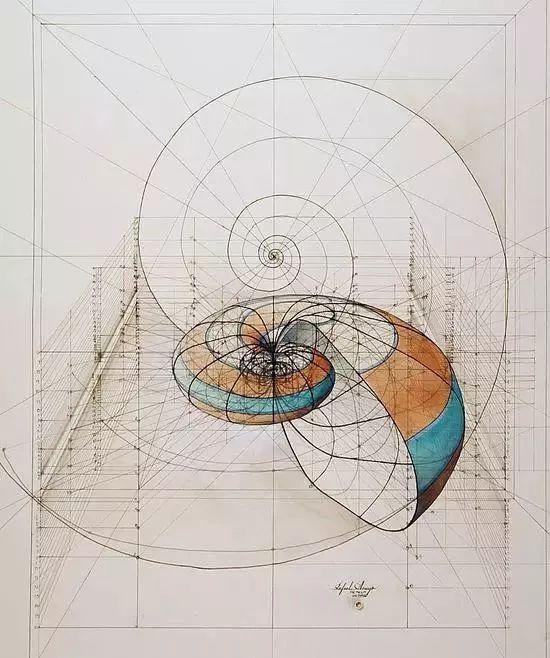
by Rafael Araujo
中国艺术家朱晓光通过抽象模拟影响作品,尝试在数学符号不断计算的过程中,寻求数学可视化与感官之间的关系。Tangent函数在空间中会有怎样的表达?数字将带给人全新感受。
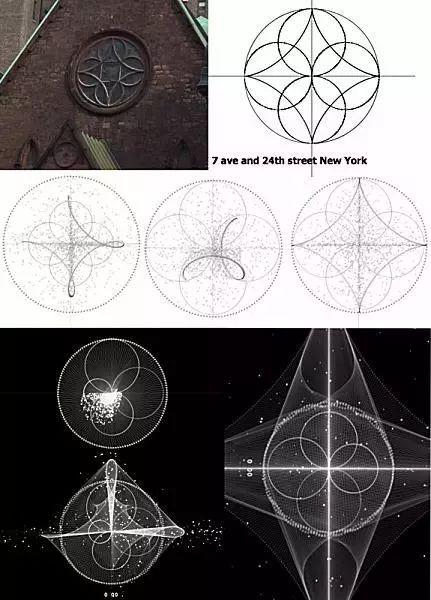 by Zhu Xiaoguang
by Zhu Xiaoguang
by Zhu Xiaoguang
看到这里你可能会觉得数学本来就很难懂,艺术又很难懂,两者加起来就更是难以理解!但其实,并不一定需要把这件事想的太过复杂或者严肃。实在不行也 可以求助于身边学习过数学或者程序的小伙伴,几分钟时间,讲不定你就可以见到下面这样迷幻小作品了呢!而下一个艺术家或许现在就在你身边读!数!学!